Responsibilities part three - joint resistance in hollow section trusses
Welcome to the most trivial hill upon which I will gladly die. Also, when I say trivial really I’m trying to manipulate you a little with self-deprecation. It’s not trivial; this issue is a constant pain in my proverbial butt-weld. This is in fact, to me, The Big One.
Much like an item mentioned previously, the web-to-flange welds in plate girders, it’s hard to see how the responsibility of this particular design element ever moved from consultant to fabricator. In fact, both situations are directly analogous. I hope to persuade all who read this missive to join me on my hill, trivial or otherwise.
Ok - so what’s got your knickers in a twist?
I’m going to lay this out one step a time as if I’m Hercule Poirot himself explaining to the reader exactly how events must have unfolded so as to arrive at the unavoidable conclusion that he is (or in this case I am) correct. Let’s begin at precisely the wrong end: the assumed and false denouement, the thing that has, in fact, got my knickers in a twist.
The claim: the steel fabricator is expected to always be able to connect up a truss designed by a third party
Oof. That hurts even just to look at.
When trusses are designed by consultants, they are presented to the fabricator as a finished item that simply needs to be connected up. If you’re lucky you will receive connection loads marked on the members of any truss, but usually you are given a table with just the maximum loadings for any given section size. You are then expected to “just connect it all up” whilst “just making it all work”.
Starting at the start, I will show you why that is almost always impossible, and why we fabricators find ourselves entangled in a design process which should have been completed long before we are brought onto a project.
First we must ask ourselves: What exactly is a truss?
A truss, for the purposes of today’s article, can be thought of as a single, large structural element made up of smaller elements. The simplest form of truss is the pin truss, and to keep this article at a sensible word count, this type alone will serve perfectly as our example for the day.
You’ve definitely seen them in the wild. They look like this:
Or this:
Or even this:
But engineers prefer to think of them as looking like this:
You see the thing about pin trusses is that they can be shown to follow very simple rules if we pretend they are made of infinitely thin lines, the lines all meet at common points, and every joint occurs at a purely pinned connection (hence the name).
To allow us to talk about the various parts of the truss we have specific names for the main elements. We usually call the horizontal parts booms or chords, and we usually refer to the other parts as the internals, though sometimes we call them the diagonals and verticals depending on their orientation. We call the intersection points nodes.
In pin trusses, as long certain rules are followed the lines themselves never bend; they only experience either compression or tension. What all of those rules are isn’t important for this discussion, but the one about members all meeting at a common pinned node is.
Excellent. We have now described an idealised model of a pin truss made up of line elements connected at pin joints. We know that the truss itself acts like one big element, and in our case that element will be analogous to a beam. And, because I am masquerading as Hercule Poirot I invite you now to imagine me fastidiously straightening the various items on my desk before taking a deep breath and barrelling on.
I’m with you so far, but what does this have to do with connections?
What this has to do with connections is the tension between the ideal and the real.
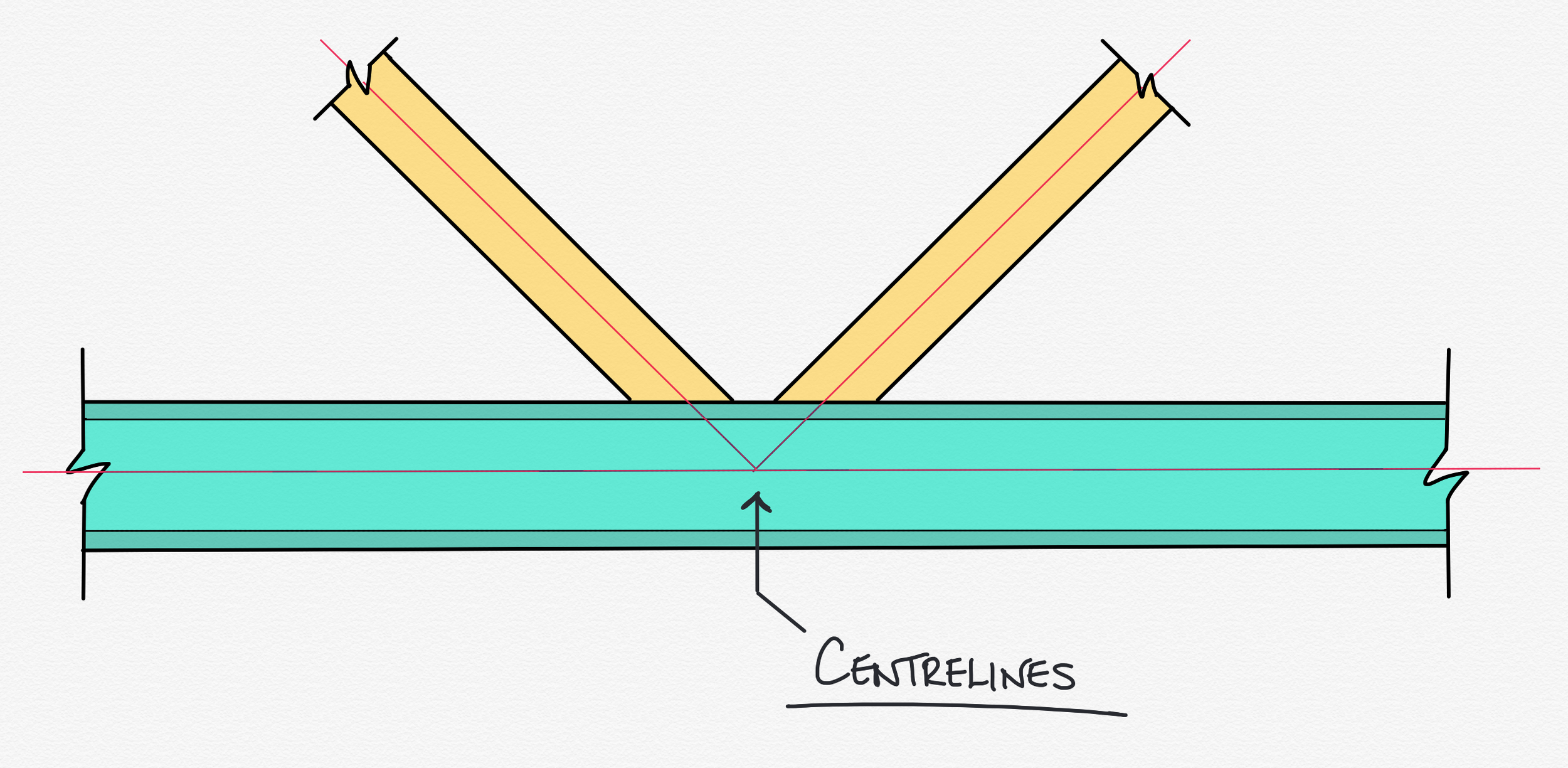
When we draw those infinitely thin lines representing the parts of the truss, we draw them down the centreline of the real lump of metal it represents, like this:
Which is fine - we do this all the time. What matters is that it is easy to forget at the design stage that those lines represent something physical; something with shape, volume, and mass.
As per classic Poirot, I’ve sneakily held something back. Something crucial, something that when you look back on it seems so obvious, but often when you’ve had your head in the detail you might forget the bigger picture.
There are rules about how those physical chunks of metal can and cannot be connected. Some of them are simple, common sense rules, and some of them a little more complex, but they are there, they are required, and they are entirely unavoidable. Let’s get on and take a look: the simplest rules to understand from a common sense perspective are the geometric validity rules, and those about member classification.
Rules part one: Geometric validity rules. Specifically, eccentricity
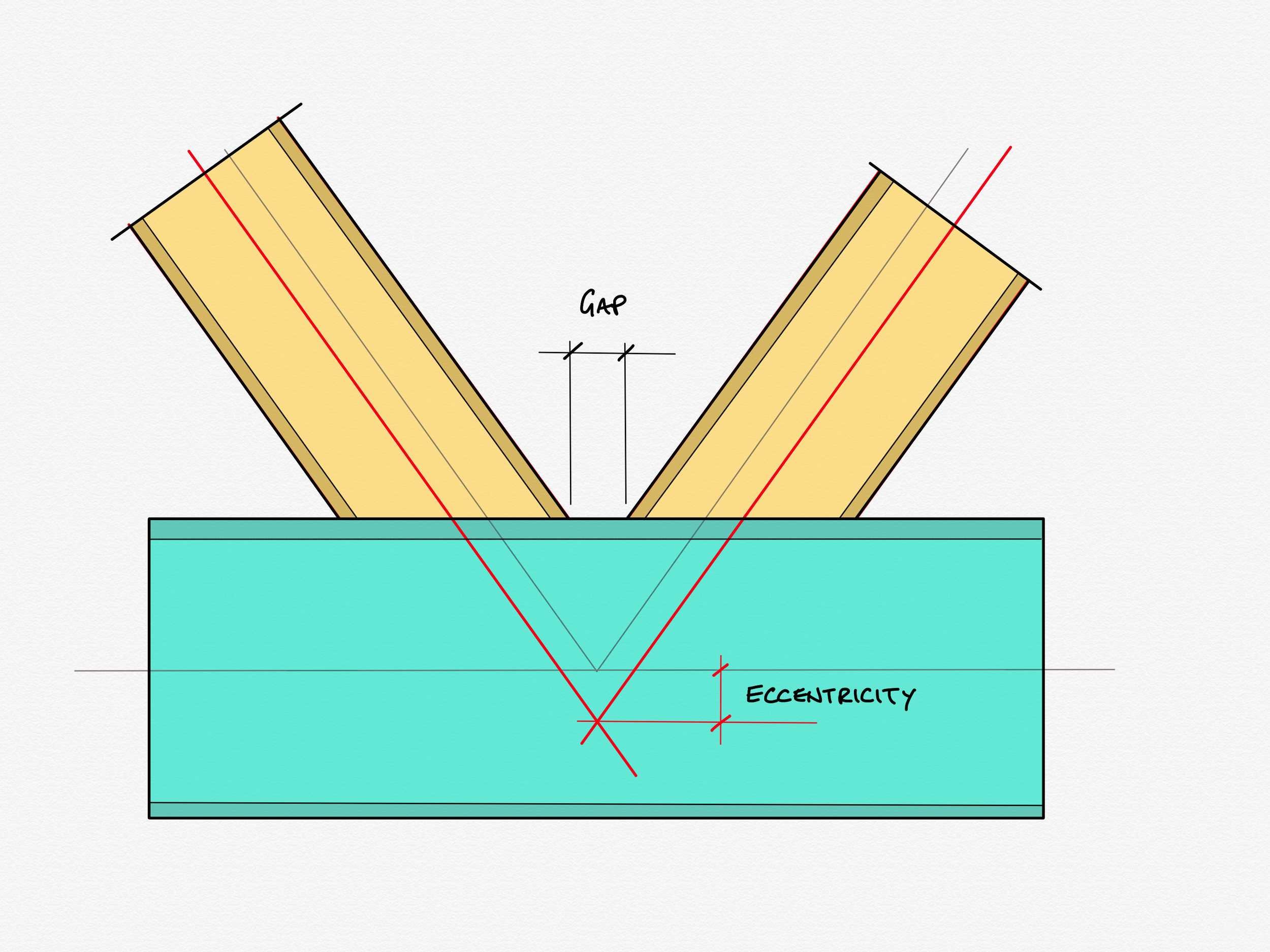
Depending on the size and angle of the diagonals and verticals, rules about maximum or minimum gaps or overlaps between members might end up broken, and things need to be shuffled about slightly to accommodate. The way that you move them to make them valid is usually to move the intersection points of the diagonals away from the nodes. This causes what we call eccentricity - see below:
Looks ok? Nothing to worry about? Let’s put some metal on those centreline bones...
Ah. Whilst this might look ok, it is in fact... not. Not only does it fall outside the geometric limits, it is impossible to fabricate, as it requires laying weld on top of weld. We have to alter the geometry to make this valid.
One solution is to pull the node apart like so, creating a decent gap between the noses of the diagonals. Alternatively the members could be overlapped even more, however that is more expensive to fabricate, as it means double cutting one of the diagonals.
Hopefully this starts to ring alarm bells.
If we “un-node” a joint sufficiently, we start to creep away from our idealised model to something a bit more… flimsy.
There a suite of formulae that comprise the CIDECT guide to truss connections which govern exactly how eccentric a connection is allowed to become before it is necessary to take account of the secondary bending induced in the booms, and the overall stiffness of the joints, and the overall stiffness of the whole truss. You can see an extract of the CIDECT guide below showing the validity limits we are forced to work to:
Here we see demonstrated a common problem: It is extremely rare that a truss is sent to our office that needs no alteration. I can think of only a couple of instances in the last decade or so where I have not had to send alterations like this back for review.
Rules part two: Member classification
As usual, I’m going to overlook many details and caveats in this next paragraph to avoid layer up on layer of footnote, and to get to the conclusion before I lose you all. Let’s just get going and crash on through regardless.
Member classification is, on a surface level, even easier to understand than noding. Members are broken into 4 classes based on their chunkiness, with Class 1 being the most chunksome, and Class 4 being the most flappy. The rule is that members in hollow section trusses must be either Class 1 or Class 2. Lower class members are deemed to be too flimsy to play nicely.
This rule is not as often broken as the geometric ones, but it does happen.
The denouement
Mes enfants.
Sorry, couldn’t resist.
We arrive here at the denouement. The chapter where Papa Poirot assembles all the suspects, and leads you through the hidden story - the narrative that happened while you weren’t looking.
We start with the simple question: “who is repsonsible for what?”.
The truss designer is responsible for the overall meta-member itself. If someone other than they were to sabotage the strength of that finished truss, for example to cut pieces out, or to substitute weaker material the designer would be upset, non? Of course they would. They would act to prevent such a thing occurring.
Therefore:
If the truss designer were to send his truss to be connected up by a third party, and that same third party were forced to make changes that had a detrimental effect on the performance of the final member, the original designer would be equally as troubled, n’est-ce pas?
As it transpires: non.
Truss designers regularly send their designs out to be fabricated, unaware that those designs are unfinished. They physically cannot be made to the desired specification, and must be altered, and often to some degree of detriment to the truss as whole. Is it right that some third party, completely disconnected from the design requirements of the truss as whole is left to propose alterations? The fabricator will not know nearly enough information to produce a finished holistic design and yet we do.
If we recall I started this series talking about a project which actually landed on my desk this year. If you think back to part one, I did in fact mention specifically that the transfer structure of this building was built from trusses, and yes, at least some of these alterations had to be made in that case. Exactly as I laid out above, time was tight, so I proposed alterations that would make the trusses valid and I was also confident the changes would have no detrimental effect on the truss as a whole. The whole exchange was brief, polite and in good spirits as all parties were aware of the time pressures on the job and everyone involved knew this was by far the quickest way to get everything done, and no egos were bruised even slightly.
It does perhaps lead us to the solution of this little mystery. How did we end up here? Are fabricators doing the work of consultants, because we are simply aware that this has become “our area of expertise” and it’s just quicker if we roll our eyes and do some of their work for them? Is it a slippery slope that we continue to step onto every time a truss lands in our office and we don’t send a stock response of “can you please confirm that all CIDECT validity checks have been carried out? Any reconfiguration will constitute a variation to our works and incur a cost”?
Perhaps.
I am aware it’s very difficult habit to break. My role as department lead/fictional Belgian detective requires me to react to ever changing circumstance but usually the default position, particularly with trusses, is that the fab shop want the fabrication drawings as early as possible. Trusses are high value items which attract high fabrication hours, so naturally the shop wants them early in the fab programme. If my production director is rightly pressuring my design team to do what they can to resolve truss nodes early to get them into the shop, my best course of action is to do what I can to get the design finished such that we can get them into production. Is this good for everyone involved? Evidently not. I am doing extra work that isn’t mine to do, but on the other hand I am achieveing a more important goal outside of my own narrow ones. Would a firmer stance be better for a fabricator, or would it both slow us down and gain us a reputation for unnecessary belligerence? I’ll end on something very un-Poirot like:
Je ne sais pas.